재귀란 무엇일까요?
구글의 사전적 의미로
트리 안에 있는 수를 검색할 때 재귀 알고리즘을 사용해서 보다 쉽게 진행할 수 있습니다.
또 다른 예로 1 부터 n까지 모든 자연수의 합을 구해봅시다.
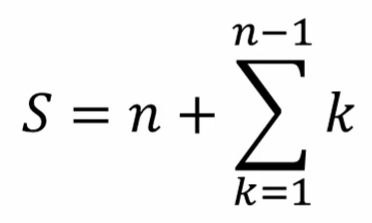
따라서 이를 함수로 표현하면
def sum(n):
return n + sum(n-1) 이 가능하는 것이죠.
다만 이를 사용할 때 주의할 게 있습니다. 무한정적인 재귀를 제한해주어야 한다는 것이죠!
def sum(n):
if n <=1:
return n
else:
return n + sum(n-1)
이런 식으로 종결 조건을 꼭 주어져야 한다는 것입니다.
재귀 알고리즘의 효율은 O(n) 시간 복잡도를 가집니다. n이 커질 때마다 시간이 더 걸리겠죠.
다만 지속적으로 함수를 호출해야하기 때문에 효율이 낮을 수 있습니다.
이를 활용한 연습 문제로 Fibonacci 순열을 구하는 코드를 짜보도록 하겠습니다.
피보나치 순열은
F0 = 0, F1= 1 일 때 Fn = Fn-1 + Fn-2, n>=2 가 성립하는 식입니다.
재귀를 사용했을 경우와 반복문을 사용할 경우를 나눠서 작성해보도록 합니다.
def solution(x):
if x < 0:
return 0
elif x == 1:
return 1
else:
return solution(x-1) + solution(x-2)위 코드는 재귀함수 입니다.
if n <= 1:
return n 이 더 좋을 겁니다!
반복문은 패스하겠습니다...
재귀 알고리즘 - 응용
문제: n개의 서로 다른 원소에서 m개를 택하는 경우의 수

라고 합니다
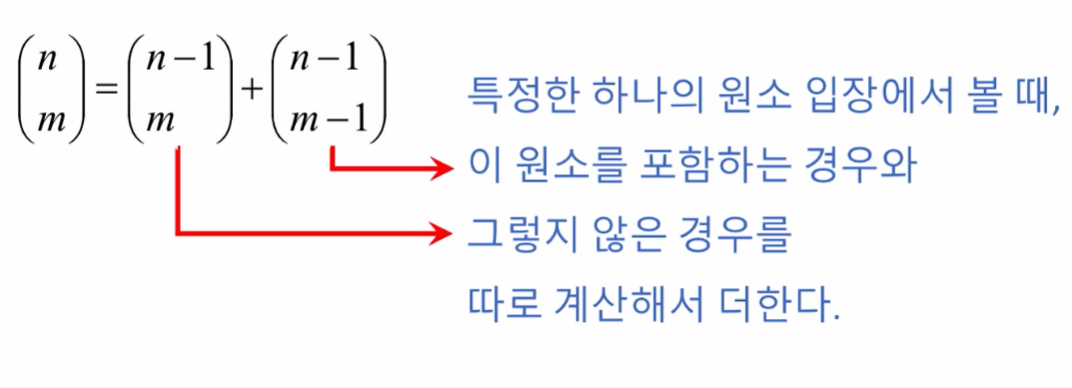
라고 하네요...
Trivial Case를 고려해서 코드를 짜면

위와 같습니다. 사람이 읽기는 편하지만 효율성 측면에서는 떨어진다고 할 수 있습니다.
재귀함수는 중복된 함수를 많이 호출하기 때문이죠.
하지만 사람이 생각하는 방식을 표현할 수 있다는 관점에서 유용하다고 할 수 있습니다.
문제 : 하노이의 탑
음... 고민을 해봐야겠죠...?
또 다른 연습 문제 입니다.
재귀적 이진 탐색 문제입니다.
주의할 점이 있습니다.
"x not in L 은 리스트 L 전체를 대상으로 원소를 하나씩 x 와 비교하는 연산으로 이루어집니다. 따라서 리스트 길이에 비례하는 시간을 소요합니다"
따라서 x not in L을 사용하면 효율성 테스트에서 걸릴 수 있습니다.
def solution(L, x, l, u):
if l > u:
return -1
mid = (l + u) // 2
if x == L[mid]:
return mid
elif x < L[mid]:
return solution(L, x, l, mid-1)
else:
return solution(L, x, mid+1, u)따라서 위와 같이 작성해야 하는데 l > u 는 재귀함수에서 x가 mid랑 같은 값이 아닐 경우 반복적인 재귀로 발생하는 경우로 x 가 list L에 없을 경우 발생하는 것을 의미합니다.
x not in L을 사용하는 자체는 재귀함수에 대한 이해 부족으로 나올 수 있는 생각이라고 하시네요 ㅠㅜㅠ
정말 쉽지 않은 알고리즘 같습니다.
이 정도로 어려워하다니... 암담하지만 그래도 계속 하겠습니다.
Just do it.
댓글